This tutorial provides a concise explanation of monads and demonstrates their implementation in five popular programming languages: JavaScript, Python, Ruby, Swift, and Scala. Whether you’re seeking to understand monads in a specific language or compare different implementations, this guide has you covered!
By leveraging monads, you can effectively eliminate various bugs, including null-pointer exceptions, unhandled exceptions, and race conditions.
This tutorial covers the following:
- An overview of category theory
- The definition of a monad
- Implementations of Option (“Maybe”), Either, and Future monads, accompanied by a sample program illustrating their use in JavaScript, Python, Ruby, Swift, and Scala
Let’s embark on this journey! Our first destination is category theory, the foundation of monads.
Introduction to Category Theory
Category theory, a mathematical field that gained prominence in the mid-20th century, underpins many functional programming concepts, including monads. We’ll briefly examine some category theory concepts relevant to software development.
Three core concepts define a category:
- Type represents data types as seen in statically typed languages, such as
Int,String,Dog,Cat, etc. - Functions establish connections between types, visualized as arrows from one type to another (or to themselves). A function $f$ from type $T$ to type $U$ is denoted as $f: T \to U$, analogous to a programming function taking a $T$ type argument and returning a $U$ type value.
- Composition combines existing functions to create new ones, denoted by the $\cdot$ operator. In a category, for any functions $f: T \to U$ and $g: U \to V$, there exists a unique function $h: T \to V$ denoted as $f \cdot g$. Essentially, this operation maps a pair of functions to a new one. Programming languages readily support this operation. For example, given a function $strlen: String \to Int$ returning the length of a string and another function $even: Int \to Boolean$ checking for even numbers, we can create a function $even{\_}strlen: String \to Boolean$ to determine if a string’s length is even. Here, $even{\_}strlen = even \cdot strlen$. Composition implies:
- Associativity: $f \cdot g \cdot h = (f \cdot g) \cdot h = f \cdot (g \cdot h)$
- Identity function existence: $\forall T: \exists f: T \to T$. In simpler terms, for every type $T$, there’s a function mapping $T$ to itself.
Let’s visualize a simple category:
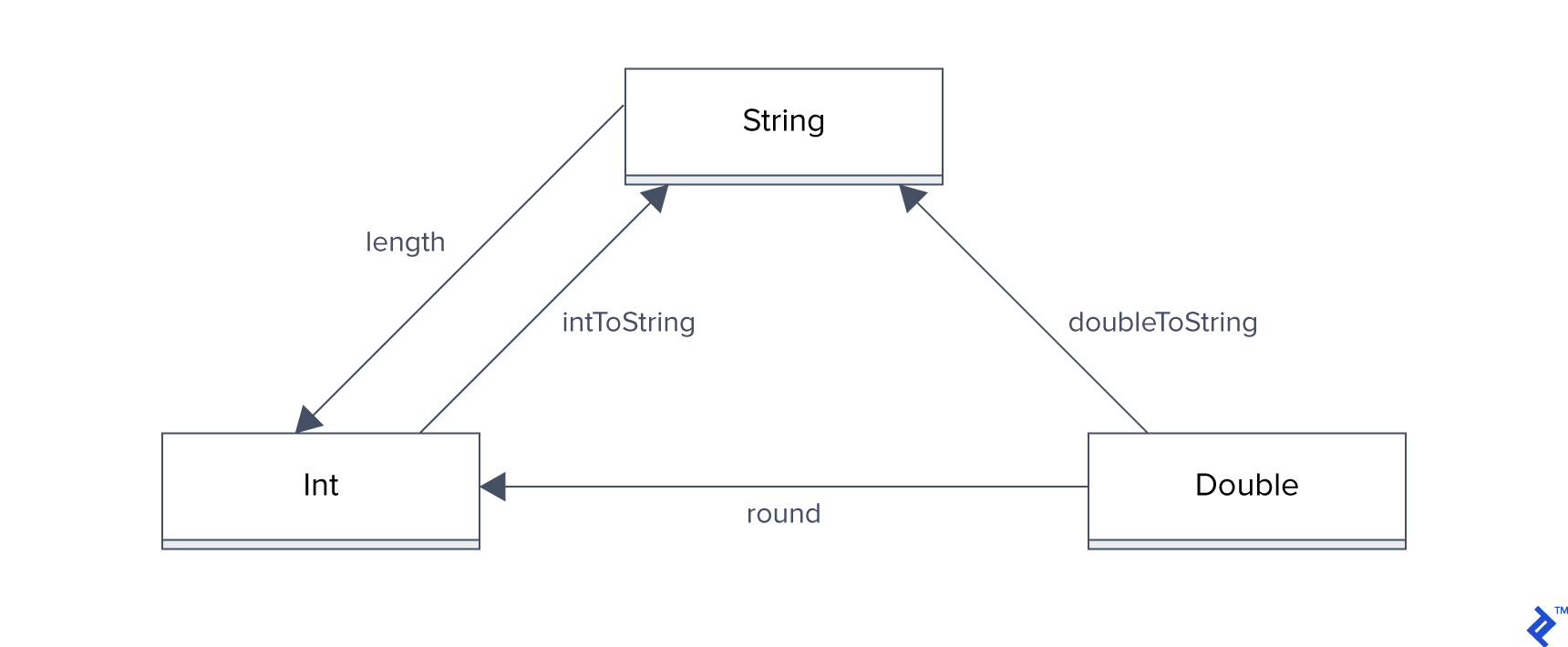
Note: We assume Int, String, and other types here are non-nullable, meaning the null value is absent.
Note 2: This diagram represents only a portion of a category, sufficient for our discussion as it includes the essential elements without unnecessary complexity. A complete category would also include composed functions like $roundToString: Double \to String = intToString \cdot round$ to satisfy the composition requirement.
You’ll observe that functions within this category are quite basic. In fact, it’s nearly impossible to introduce bugs into them. There are no nulls, no exceptions—just arithmetic and memory operations. The only potential issues arise from processor or memory failures, requiring program termination—a rare occurrence.
Having all our code operate at this level of stability would be ideal! However, real-world applications require functionalities like I/O. This is where monads come to the rescue: They encapsulate unstable operations within small, well-tested code units, enabling stable calculations throughout your application!
Enter Monads
Let’s refer to unstable behavior like I/O as a side effect. Our goal is to work with previously defined functions like length and types like String in a stable manner, even with this side effect.
Starting with an empty category $M[A]$, we aim to create a category containing values with a specific side effect and values without any. Initially, this category is empty and not very useful. To enhance its utility, we’ll follow these steps:
- Populate it with values from category $A$ types like
String,Int,Double, etc. (green boxes in the diagram below). - With these values, meaningful operations are still limited. So, for each function $f: T \to U$ from $A$, we’ll create a function $g: M[T] \to M[U]$ (blue arrows in the diagram below). This enables us to perform the same operations on values in category $M[A]$ as in category $A$.
- This new category $M[A]$ introduces a new class of functions with the signature $h: T \to M[U]$ (red arrows in the diagram below), arising from promoting values in step one. These functions distinguish working with $M[A]$ from working with $A$. The final step ensures these functions operate seamlessly on types in $M[A]$, allowing us to derive function $m: M[T] \to M[U]$ from $h: T \to M[U]$.
![Creating a new category: Categories A and M[A], plus a red arrow from A's Double to M[A]'s Int, labelled "roundAsync". M[A] reuses every value and function of A at this point.](https://assets.toptal.io/images?url=https%3A%2F%2Fuploads.toptal.io%2Fblog%2Fimage%2F127403%2Ftoptal-blog-image-1540211900150-82f554ff98243b2ef4c9f00c13f64c14.png)
We define two methods to promote values of $A$ types to $M[A]$ types: one without side effects and one with.
- The first, called $pure$, applies to each value of a stable category: $pure: T \to M[T]$. The resulting $M[T]$ values have no side effects, hence the name $pure$. For instance, in an I/O monad, $pure$ immediately returns a value without the possibility of failure.
- The second, called $constructor$, unlike $pure$, returns $M[T]$ with potential side effects. For example, an async I/O monad’s $constructor$ could fetch data from the web, returning it as a
String. The returned value would have the type $M[String]$ in this case.
With these two promotion methods, you, the programmer, decide which function to use based on the program’s requirements. Consider fetching the HTML page from https://www.toptal.com/javascript/option-maybe-either-future-monads-js. You create a function $fetch$. Due to potential issues like network failures, the return type is $M[String]$. The function signature becomes $fetch: String \to M[String]$, using the $constructor$ for $M$ within its body.
For testing, you create a mock function $fetchMock: String \to M[String]$. While the signature remains the same, $fetchMock$ directly injects the HTML page without any unstable network operations, using $pure$ in its implementation.
Next, we need a function to safely promote any function $f$ from category $A$ to $M[A]$ (blue arrows in the diagram). This function is $map: (T \to U) \to (M[T] \to M[U])$.
We now have a category that can handle side effects (using $constructor$) and includes all functions from the stable category, ensuring their stability within $M[A]$. This introduces functions like $f: T \to M[U]$, such as $pure$, $constructor$, and combinations of these with $map$. We need a way to work with arbitrary functions in the form $f: T \to M[U]$.
To apply a function based on $f$ to $M[T]$, using $map$ would result in a function $g: M[T] \to M[M[U]]$, introducing an undesired additional category $M[M[A]]$. To address this, we introduce the $flatMap: (T \to M[U]) \to (M[T] \to M[U])$ function.
Let’s illustrate the need for $flatMap$. Assume we’ve completed step 2, having $pure$, $constructor$, and $map$. We want to fetch an HTML page from toptal.com, scan all URLs within it, and fetch those as well. We create a function $fetch: String \to M[String]$ to fetch a single URL and return its HTML page.
Applying this function to a URL gives us $x: M[String]$, the toptal.com page. After some transformations on $x$, we obtain a URL $u: M[String]$. We’d like to apply $fetch$ to $u$, but its input type is $String$, not $M[String]$. This is where $flatMap$ comes in, converting $fetch: String \to M[String]$ to $m_fetch: M[String] \to M[String]$.
Having completed all three steps, we can now compose any value transformations we need. For example, given a value $x$ of type $M[T]$ and a function $f: T \to U$, we can apply $f$ to $x$ using $map$, resulting in a value $y$ of type $M[U]$. This ensures 100% bug-free value transformations as long as $pure$, $constructor$, $map$, and $flatMap$ are implemented correctly.
Instead of handling potential issues related to side effects throughout your codebase, you only need to ensure the correct implementation of these four functions. At the end of your program, you’ll have a single $M[X]$ from which you can safely extract the value $X$ and handle any error cases.
This is essentially what a monad is: an entity implementing $pure$, $map$, and $flatMap$. (While $map$ can be derived from $pure$ and $flatMap$, its widespread use and utility warrant its inclusion in the definition.)
The Option Monad, a.k.a. the Maybe Monad
Let’s delve into the practical implementation and use of monads. Our first example, the Option monad, addresses the infamous null pointer error common in classic programming languages. Tony Hoare, the inventor of null, famously called it his “Billion Dollar Mistake”:
This has led to innumerable errors, vulnerabilities, and system crashes, which have probably caused a billion dollars of pain and damage in the last forty years.
Let’s see how we can improve upon this. The Option monad either holds a non-null value or no value at all. This resembles a null value, but with the Option monad, we can safely utilize our well-defined functions without the risk of encountering null pointer exceptions. Let’s examine implementations in various languages:
JavaScript—Option Monad/Maybe Monad
class Monad {
// pure :: a -> M a
pure = () => { throw "pure method needs to be implemented" }
// flatMap :: # M a -> (a -> M b) -> M b
flatMap = (x) => { throw "flatMap method needs to be implemented" }
// map :: # M a -> (a -> b) -> M b
map = f => this.flatMap(x => new this.pure(f(x)))
}
export class Option extends Monad {
// pure :: a -> Option a
pure = (value) => {
if ((value === null) || (value === undefined)) {
return none;
}
return new Some(value)
}
// flatMap :: # Option a -> (a -> Option b) -> Option b
flatMap = f =>
this.constructor.name === 'None' ?
none :
f(this.value)
// equals :: # M a -> M a -> boolean
equals = (x) => this.toString() === x.toString()
}
class None extends Option {
toString() {
return 'None';
}
}
// Cached None class value
export const none = new None()
Option.pure = none.pure
export class Some extends Option {
constructor(value) {
super();
this.value = value;
}
toString() {
return `Some(${this.value})`
}
}
Python—Option Monad/Maybe Monad
class Monad:
# pure :: a -> M a
@staticmethod
def pure(x):
raise Exception("pure method needs to be implemented")
# flat_map :: # M a -> (a -> M b) -> M b
def flat_map(self, f):
raise Exception("flat_map method needs to be implemented")
# map :: # M a -> (a -> b) -> M b
def map(self, f):
return self.flat_map(lambda x: self.pure(f(x)))
class Option(Monad):
# pure :: a -> Option a
@staticmethod
def pure(x):
return Some(x)
# flat_map :: # Option a -> (a -> Option b) -> Option b
def flat_map(self, f):
if self.defined:
return f(self.value)
else:
return nil
class Some(Option):
def __init__(self, value):
self.value = value
self.defined = True
class Nil(Option):
def __init__(self):
self.value = None
self.defined = False
nil = Nil()
Ruby—Option Monad/Maybe Monad
class Monad
# pure :: a -> M a
def self.pure(x)
raise StandardError("pure method needs to be implemented")
end
# pure :: a -> M a
def pure(x)
self.class.pure(x)
end
def flat_map(f)
raise StandardError("flat_map method needs to be implemented")
end
# map :: # M a -> (a -> b) -> M b
def map(f)
flat_map(-> (x) { pure(f.call(x)) })
end
end
class Option < Monad
attr_accessor :defined, :value
# pure :: a -> Option a
def self.pure(x)
Some.new(x)
end
# pure :: a -> Option a
def pure(x)
Some.new(x)
end
# flat_map :: # Option a -> (a -> Option b) -> Option b
def flat_map(f)
if defined
f.call(value)
else
$none
end
end
end
class Some < Option
def initialize(value)
@value = value
@defined = true
end
end
class None < Option
def initialize()
@defined = false
end
end
$none = None.new()
Swift—Option Monad/Maybe Monad
import Foundation
enum Maybe<A> {
case None
case Some(A)
static func pure<B>(_ value: B) -> Maybe<B> {
return .Some(value)
}
func flatMap<B>(_ f: (A) -> Maybe<B>) -> Maybe<B> {
switch self {
case .None:
return .None
case .Some(let value):
return f(value)
}
}
func map<B>(f: (A) -> B) -> Maybe<B> {
return self.flatMap { type(of: self).pure(f($0)) }
}
}
Scala—Option Monad/Maybe Monad
import language.higherKinds
trait Monad[M[_]] {
def pure[A](a: A): M[A]
def flatMap[A, B](ma: M[A])(f: A => M[B]): M[B]
def map[A, B](ma: M[A])(f: A => B): M[B] =
flatMap(ma)(x => pure(f(x)))
}
object Monad {
def apply[F[_]](implicit M: Monad[F]): Monad[F] = M
implicit val myOptionMonad = new Monad[MyOption] {
def pure[A](a: A) = MySome(a)
def flatMap[A, B](ma: MyOption[A])(f: A => MyOption[B]): MyOption[B] = ma match {
case MyNone => MyNone
case MySome(a) => f(a)
}
}
}
sealed trait MyOption[+A] {
def flatMap[B](f: A => MyOption[B]): MyOption[B] =
Monad[MyOption].flatMap(this)(f)
def map[B](f: A => B): MyOption[B] =
Monad[MyOption].map(this)(f)
}
case object MyNone extends MyOption[Nothing]
case class MySome[A](x: A) extends MyOption[A]
We start by implementing a base Monad class for all our monad implementations. This simplifies things significantly, as implementing just pure and flatMap for a specific monad provides access to many other methods automatically (limited to map in our examples for brevity, but generally including useful methods like sequence and traverse for handling arrays of Monads).
We express map as a composition of pure and flatMap. Examining flatMap’s signature, $flatMap: (T \to M[U]) \to (M[T] \to M[U])$, reveals its similarity to $map: (T \to U) \to (M[T] \to M[U])$. The only difference is the additional $M$ in the middle, which we address using pure to convert $U$ into $M[U]$. This way, we express map in terms of flatMap and pure.
This approach works seamlessly in Scala due to its advanced type system and in dynamically typed languages like JS, Python, and Ruby. However, Swift, being statically typed and lacking advanced type features like higher-kinded types, requires a separate map implementation for each monad.
Note that the Option monad is already a standard feature in languages like Swift and Scala, explaining the slight name variations in our implementations.
With our base Monad class in place, let’s move on to the Option monad implementations. As mentioned earlier, the core concept is that Option either holds a value (Some) or not (None).
The pure method simply promotes a value to Some, while flatMap checks the Option’s current state. If it’s None, it returns None. If it’s Some with an underlying value, it extracts this value, applies f() to it, and returns the result.
Using just these two functions and map, encountering a null pointer exception becomes impossible. (A potential issue could arise within our flatMap implementation, but that’s just a few lines of code checked once. Afterward, we can confidently use our Option monad implementation throughout our codebase without fearing null pointer exceptions.)
The Either Monad
Next up is the Either monad, essentially an Option monad with Some renamed to Right and None renamed to Left. However, Left in this case can also hold a value.
This is useful for representing exceptions. If an exception occurs, the Either value will be Left(Exception). The flatMap function halts progression if the value is Left, mimicking exception throwing behavior: If an exception happens, further execution stops.
JavaScript—Either Monad
import Monad from './monad';
export class Either extends Monad {
// pure :: a -> Either a
pure = (value) => {
return new Right(value)
}
// flatMap :: # Either a -> (a -> Either b) -> Either b
flatMap = f =>
this.isLeft() ?
this :
f(this.value)
isLeft = () => this.constructor.name === 'Left'
}
export class Left extends Either {
constructor(value) {
super();
this.value = value;
}
toString() {
return `Left(${this.value})`
}
}
export class Right extends Either {
constructor(value) {
super();
this.value = value;
}
toString() {
return `Right(${this.value})`
}
}
// attempt :: (() -> a) -> M a
Either.attempt = f => {
try {
return new Right(f())
} catch(e) {
return new Left(e)
}
}
Either.pure = (new Left(null)).pure
Python—Either Monad
from monad import Monad
class Either(Monad):
# pure :: a -> Either a
@staticmethod
def pure(value):
return Right(value)
# flat_map :: # Either a -> (a -> Either b) -> Either b
def flat_map(self, f):
if self.is_left:
return self
else:
return f(self.value)
class Left(Either):
def __init__(self, value):
self.value = value
self.is_left = True
class Right(Either):
def __init__(self, value):
self.value = value
self.is_left = False
Ruby—Either Monad
require_relative './monad'
class Either < Monad
attr_accessor :is_left, :value
# pure :: a -> Either a
def self.pure(value)
Right.new(value)
end
# pure :: a -> Either a
def pure(value)
self.class.pure(value)
end
# flat_map :: # Either a -> (a -> Either b) -> Either b
def flat_map(f)
if is_left
self
else
f.call(value)
end
end
end
class Left < Either
def initialize(value)
@value = value
@is_left = true
end
end
class Right < Either
def initialize(value)
@value = value
@is_left = false
end
end
Swift—Either Monad
import Foundation
enum Either<A, B> {
case Left(A)
case Right(B)
static func pure<C>(_ value: C) -> Either<A, C> {
return Either<A, C>.Right(value)
}
func flatMap<D>(_ f: (B) -> Either<A, D>) -> Either<A, D> {
switch self {
case .Left(let x):
return Either<A, D>.Left(x)
case .Right(let x):
return f(x)
}
}
func map<C>(f: (B) -> C) -> Either<A, C> {
return self.flatMap { Either<A, C>.pure(f($0)) }
}
}
Scala—Either Monad
package monad
sealed trait MyEither[+E, +A] {
def flatMap[EE >: E, B](f: A => MyEither[EE, B]): MyEither[EE, B] =
Monad[MyEither[EE, ?]].flatMap(this)(f)
def map[EE >: E, B](f: A => B): MyEither[EE, B] =
Monad[MyEither[EE, ?]].map(this)(f)
}
case class MyLeft[E](e: E) extends MyEither[E, Nothing]
case class MyRight[A](a: A) extends MyEither[Nothing, A]
// ...
implicit def myEitherMonad[E] = new Monad[MyEither[E, ?]] {
def pure[A](a: A) = MyRight(a)
def flatMap[A, B](ma: MyEither[E, A])(f: A => MyEither[E, B]): MyEither[E, B] = ma match {
case MyLeft(a) => MyLeft(a)
case MyRight(b) => f(b)
}
}
Catching exceptions is also straightforward: simply map Left to Right. (We omit this in our examples for brevity.)
The Future Monad
Finally, let’s explore the Future monad. This monad acts as a container for a value available either immediately or in the near future. Using map and flatMap, you can create chains of Futures that wait for a Future value to resolve before executing the next dependent code block. This resembles the concept of Promises in JS.
Our objective is to bridge existing asynchronous APIs across different languages to a consistent base. Callbacks in $constructor$ offer the most straightforward design approach.
While callbacks introduced the “callback hell” problem in JavaScript and other languages, this won’t be an issue for us thanks to monads. In fact, the Promise object in JavaScript, designed to address callback hell, is a monad itself!
Let’s examine the Future monad’s constructor signature:
constructor :: ((Either err a -> void) -> void) -> Future (Either err a)
Breaking it down, we first define:
type Callback = Either err a -> void
Here, Callback is a function accepting either an error or a resolved value as an argument and returning nothing. Now the signature becomes:
constructor :: (Callback -> void) -> Future (Either err a)
We need to provide a function that returns nothing and triggers a callback once the asynchronous computation resolves to either an error or a value. This enables easy bridging for any language.
Turning to the Future monad’s internal structure, the key idea is a cache variable. This variable stores a value if the Future monad is resolved and remains empty otherwise. Subscribing to the Future with a callback triggers it immediately if the value is resolved. Otherwise, the callback is added to a subscribers list.
Upon Future resolution, each callback in the list is triggered exactly once with the resolved value in a separate thread (or as the next function in the event loop for JS). Careful synchronization primitive usage is crucial here to prevent race conditions.
The basic flow involves initiating the asynchronous computation provided as the constructor argument and pointing its callback to our internal callback method. Simultaneously, you can subscribe to the Future monad, adding your callbacks to the queue. Once the computation completes, the internal callback method invokes all queued callbacks. This approach closely resembles the asynchronous handling in Reactive Extensions (RxJS, RxSwift, etc.).
The Future monad’s public API consists of pure, map, and flatMap, similar to previous monads. Additionally, we include a couple of convenient methods:
-
asynctakes a synchronous blocking function and executes it in a separate thread. traversetakes an array of values and a function mapping a value to aFuture. It returns aFutureof an array containing resolved values.
Let’s see this in action:
JavaScript—Future Monad
import Monad from './monad';
import { Either, Left, Right } from './either';
import { none, Some } from './option';
export class Future extends Monad {
// constructor :: ((Either err a -> void) -> void) -> Future (Either err a)
constructor(f) {
super();
this.subscribers = [];
this.cache = none;
f(this.callback)
}
// callback :: Either err a -> void
callback = (value) => {
this.cache = new Some(value)
while (this.subscribers.length) {
const subscriber = this.subscribers.shift();
subscriber(value)
}
}
// subscribe :: (Either err a -> void) -> void
subscribe = (subscriber) =>
(this.cache === none ? this.subscribers.push(subscriber) : subscriber(this.cache.value))
toPromise = () => new Promise(
(resolve, reject) =>
this.subscribe(val => val.isLeft() ? reject(val.value) : resolve(val.value))
)
// pure :: a -> Future a
pure = Future.pure
// flatMap :: (a -> Future b) -> Future b
flatMap = f =>
new Future(
cb => this.subscribe(value => value.isLeft() ? cb(value) : f(value.value).subscribe(cb))
)
}
Future.async = (nodeFunction, ...args) => {
return new Future(cb =>
nodeFunction(...args, (err, data) => err ? cb(new Left(err)) : cb(new Right(data)))
);
}
Future.pure = value => new Future(cb => cb(Either.pure(value)))
// traverse :: [a] -> (a -> Future b) -> Future [b]
Future.traverse = list => f =>
list.reduce(
(acc, elem) => acc.flatMap(values => f(elem).map(value => [...values, value])),
Future.pure([])
)
Python—Future Monad
from monad import Monad
from option import nil, Some
from either import Either, Left, Right
from functools import reduce
import threading
class Future(Monad):
# __init__ :: ((Either err a -> void) -> void) -> Future (Either err a)
def __init__(self, f):
self.subscribers = []
self.cache = nil
self.semaphore = threading.BoundedSemaphore(1)
f(self.callback)
# pure :: a -> Future a
@staticmethod
def pure(value):
return Future(lambda cb: cb(Either.pure(value)))
def exec(f, cb):
try:
data = f()
cb(Right(data))
except Exception as err:
cb(Left(err))
def exec_on_thread(f, cb):
t = threading.Thread(target=Future.exec, args=[f, cb])
t.start()
def async(f):
return Future(lambda cb: Future.exec_on_thread(f, cb))
# flat_map :: (a -> Future b) -> Future b
def flat_map(self, f):
return Future(
lambda cb: self.subscribe(
lambda value: cb(value) if (value.is_left) else f(value.value).subscribe(cb)
)
)
# traverse :: [a] -> (a -> Future b) -> Future [b]
def traverse(arr):
return lambda f: reduce(
lambda acc, elem: acc.flat_map(
lambda values: f(elem).map(
lambda value: values + [value]
)
), arr, Future.pure([]))
# callback :: Either err a -> void
def callback(self, value):
self.semaphore.acquire()
self.cache = Some(value)
while (len(self.subscribers) > 0):
sub = self.subscribers.pop(0)
t = threading.Thread(target=sub, args=[value])
t.start()
self.semaphore.release()
# subscribe :: (Either err a -> void) -> void
def subscribe(self, subscriber):
self.semaphore.acquire()
if (self.cache.defined):
self.semaphore.release()
subscriber(self.cache.value)
else:
self.subscribers.append(subscriber)
self.semaphore.release()
Ruby—Future Monad
require_relative './monad'
require_relative './either'
require_relative './option'
class Future < Monad
attr_accessor :subscribers, :cache, :semaphore
# initialize :: ((Either err a -> void) -> void) -> Future (Either err a)
def initialize(f)
@subscribers = []
@cache = $none
@semaphore = Queue.new
@semaphore.push(nil)
f.call(method(:callback))
end
# pure :: a -> Future a
def self.pure(value)
Future.new(-> (cb) { cb.call(Either.pure(value)) })
end
def self.async(f, *args)
Future.new(-> (cb) {
Thread.new {
begin
cb.call(Right.new(f.call(*args)))
rescue => e
cb.call(Left.new(e))
end
}
})
end
# pure :: a -> Future a
def pure(value)
self.class.pure(value)
end
# flat_map :: (a -> Future b) -> Future b
def flat_map(f)
Future.new(-> (cb) {
subscribe(-> (value) {
if (value.is_left)
cb.call(value)
else
f.call(value.value).subscribe(cb)
end
})
})
end
# traverse :: [a] -> (a -> Future b) -> Future [b]
def self.traverse(arr, f)
arr.reduce(Future.pure([])) do |acc, elem|
acc.flat_map(-> (values) {
f.call(elem).map(-> (value) { values + [value] })
})
end
end
# callback :: Either err a -> void
def callback(value)
semaphore.pop
self.cache = Some.new(value)
while (subscribers.count > 0)
sub = self.subscribers.shift
Thread.new {
sub.call(value)
}
end
semaphore.push(nil)
end
# subscribe :: (Either err a -> void) -> void
def subscribe(subscriber)
semaphore.pop
if (self.cache.defined)
semaphore.push(nil)
subscriber.call(cache.value)
else
self.subscribers.push(subscriber)
semaphore.push(nil)
end
end
end
Swift—Future Monad
import Foundation
let background = DispatchQueue(label: "background", attributes: .concurrent)
class Future<Err, A> {
typealias Callback = (Either<Err, A>) -> Void
var subscribers: Array<Callback> = Array<Callback>()
var cache: Maybe<Either<Err, A>> = .None
var semaphore = DispatchSemaphore(value: 1)
lazy var callback: Callback = { value in
self.semaphore.wait()
self.cache = .Some(value)
while (self.subscribers.count > 0) {
let subscriber = self.subscribers.popLast()
background.async {
subscriber?(value)
}
}
self.semaphore.signal()
}
init(_ f: @escaping (@escaping Callback) -> Void) {
f(self.callback)
}
func subscribe(_ cb: @escaping Callback) {
self.semaphore.wait()
switch cache {
case .None:
subscribers.append(cb)
self.semaphore.signal()
case .Some(let value):
self.semaphore.signal()
cb(value)
}
}
static func pure<B>(_ value: B) -> Future<Err, B> {
return Future<Err, B> { $0(Either<Err, B>.pure(value)) }
}
func flatMap<B>(_ f: @escaping (A) -> Future<Err, B>) -> Future<Err, B> {
return Future<Err, B> { [weak self] cb in
guard let this = self else { return }
this.subscribe { value in
switch value {
case .Left(let err):
cb(Either<Err, B>.Left(err))
case .Right(let x):
f(x).subscribe(cb)
}
}
}
}
func map<B>(_ f: @escaping (A) -> B) -> Future<Err, B> {
return self.flatMap { Future<Err, B>.pure(f($0)) }
}
static func traverse<B>(_ list: Array<A>, _ f: @escaping (A) -> Future<Err, B>) -> Future<Err, Array<B>> {
return list.reduce(Future<Err, Array<B>>.pure(Array<B>())) { (acc: Future<Err, Array<B>>, elem: A) in
return acc.flatMap { elems in
return f(elem).map { val in
return elems + [val]
}
}
}
}
}
Scala—Future Monad
package monad
import java.util.concurrent.Semaphore
class MyFuture[A] {
private var subscribers: List[MyEither[Exception, A] => Unit] = List()
private var cache: MyOption[MyEither[Exception, A]] = MyNone
private val semaphore = new Semaphore(1)
def this(f: (MyEither[Exception, A] => Unit) => Unit) {
this()
f(this.callback _)
}
def flatMap[B](f: A => MyFuture[B]): MyFuture[B] =
Monad[MyFuture].flatMap(this)(f)
def map[B](f: A => B): MyFuture[B] =
Monad[MyFuture].map(this)(f)
def callback(value: MyEither[Exception, A]): Unit = {
semaphore.acquire
cache = MySome(value)
subscribers.foreach { sub =>
val t = new Thread(
new Runnable {
def run: Unit = {
sub(value)
}
}
)
t.start
}
subscribers = List()
semaphore.release
}
def subscribe(sub: MyEither[Exception, A] => Unit): Unit = {
semaphore.acquire
cache match {
case MyNone =>
subscribers = sub :: subscribers
semaphore.release
case MySome(value) =>
semaphore.release
sub(value)
}
}
}
object MyFuture {
def async[B, C](f: B => C, arg: B): MyFuture[C] =
new MyFuture[C]({ cb =>
val t = new Thread(
new Runnable {
def run: Unit = {
try {
cb(MyRight(f(arg)))
} catch {
case e: Exception => cb(MyLeft(e))
}
}
}
)
t.start
})
def traverse[A, B](list: List[A])(f: A => MyFuture[B]): MyFuture[List[B]] = {
list.foldRight(Monad[MyFuture].pure(List[B]())) { (elem, acc) =>
Monad[MyFuture].flatMap(acc) ({ values =>
Monad[MyFuture].map(f(elem)) { value => value :: values }
})
}
}
}
// ...
implicit val myFutureMonad = new Monad[MyFuture] {
def pure[A](a: A): MyFuture[A] =
new MyFuture[A]({ cb => cb(myEitherMonad[Exception].pure(a)) })
def flatMap[A, B](ma: MyFuture[A])(f: A => MyFuture[B]): MyFuture[B] =
new MyFuture[B]({ cb =>
ma.subscribe(_ match {
case MyLeft(e) => cb(MyLeft(e))
case MyRight(a) => f(a).subscribe(cb)
})
})
}
Notice how Future’s public API remains free of low-level details like threads, semaphores, etc. You simply provide something with a callback, and the monad takes care of the rest!
Composing a Program from Monads
Let’s build a program using our monads. We have a file containing a list of URLs and want to fetch them in parallel, truncate the responses to 200 bytes for brevity, and print the result.
First, we convert existing language APIs to monadic interfaces (using functions readFile and fetch). We then compose them into a chain to obtain the final result. Note that the chain itself remains exceptionally safe, as all the complex details are encapsulated within the monads.
JavaScript—Sample Monad Program
import { Future } from './future';
import { Either, Left, Right } from './either';
import { readFile } from 'fs';
import https from 'https';
const getResponse = url =>
new Future(cb => https.get(url, res => {
var body = '';
res.on('data', data => body += data);
res.on('end', data => cb(new Right(body)));
res.on('error', err => cb(new Left(err)))
}))
const getShortResponse = url => getResponse(url).map(resp => resp.substring(0, 200))
Future
.async(readFile, 'resources/urls.txt')
.map(data => data.toString().split("\n"))
.flatMap(urls => Future.traverse(urls)(getShortResponse))
.map(console.log)
Python—Sample Monad Program
import http.client
import threading
import time
import os
from future import Future
from either import Either, Left, Right
conn = http.client.HTTPSConnection("en.wikipedia.org")
def read_file_sync(uri):
base_dir = os.path.dirname(__file__) #<-- absolute dir the script is in
path = os.path.join(base_dir, uri)
with open(path) as f:
return f.read()
def fetch_sync(uri):
conn.request("GET", uri)
r = conn.getresponse()
return r.read().decode("utf-8")[:200]
def read_file(uri):
return Future.async(lambda: read_file_sync(uri))
def fetch(uri):
return Future.async(lambda: fetch_sync(uri))
def main(args=None):
lines = read_file("../resources/urls.txt").map(lambda res: res.splitlines())
content = lines.flat_map(lambda urls: Future.traverse(urls)(fetch))
output = content.map(lambda res: print("\n".join(res)))
if __name__ == "__main__":
main()
Ruby—Sample Monad Program
require './lib/future'
require 'net/http'
require 'uri'
semaphore = Queue.new
def read(uri)
Future.async(-> () { File.read(uri) })
end
def fetch(url)
Future.async(-> () {
uri = URI(url)
Net::HTTP.get_response(uri).body[0..200]
})
end
read("resources/urls.txt")
.map(-> (x) { x.split("\n") })
.flat_map(-> (urls) {
Future.traverse(urls, -> (url) { fetch(url) })
})
.map(-> (res) { puts res; semaphore.push(true) })
semaphore.pop
Swift—Sample Monad Program
import Foundation
enum Err: Error {
case Some(String)
}
func readFile(_ path: String) -> Future<Error, String> {
return Future<Error, String> { callback in
background.async {
let url = URL(fileURLWithPath: path)
let text = try? String(contentsOf: url)
if let res = text {
callback(Either<Error, String>.pure(res))
} else {
callback(Either<Error, String>.Left(Err.Some("Error reading urls.txt")))
}
}
}
}
func fetchUrl(_ url: String) -> Future<Error, String> {
return Future<Error, String> { callback in
background.async {
let url = URL(string: url)
let task = URLSession.shared.dataTask(with: url!) {(data, response, error) in
if let err = error {
callback(Either<Error, String>.Left(err))
return
}
guard let nonEmptyData = data else {
callback(Either<Error, String>.Left(Err.Some("Empty response")))
return
}
guard let result = String(data: nonEmptyData, encoding: String.Encoding.utf8) else {
callback(Either<Error, String>.Left(Err.Some("Cannot decode response")))
return
}
let index = result.index(result.startIndex, offsetBy: 200)
callback(Either<Error, String>.pure(String(result[..<index])))
}
task.resume()
}
}
}
var result: Any = ""
let _ = readFile("\(projectDir)/Resources/urls.txt")
.map { data -> [String] in
data.components(separatedBy: "\n").filter { (line: String) in !line.isEmpty }
}.flatMap { urls in
return Future<Error, String>.traverse(urls) { url in
return fetchUrl(url)
}
}.map { responses in
print(responses)
}
RunLoop.main.run()
Scala—Sample Monad Program
import scala.io.Source
import java.util.concurrent.Semaphore
import monad._
object Main extends App {
val semaphore = new Semaphore(0)
def readFile(name: String): MyFuture[List[String]] =
MyFuture.async[String, List[String]](filename => Source.fromResource(filename).getLines.toList, name)
def fetch(url: String): MyFuture[String] =
MyFuture.async[String, String](
uri => Source.fromURL(uri).mkString.substring(0, 200),
url
)
val future = for {
urls <- readFile("urls.txt")
entries <- MyFuture.traverse(urls)(fetch _)
} yield {
println(entries)
semaphore.release
}
semaphore.acquire
}
There you have it—monad solutions in practice. You can find the complete code for this article on GitHub.
Overhead: Done. Benefits: Ongoing
While using monads for this simple program might seem like overkill, the initial setup remains constant in size. From now on, you can write extensive asynchronous code using monads without worrying about threads, race conditions, semaphores, exceptions, or null pointers!