Approaching the creation of an interpreter from the beginning

Some argue that “everything comes down to ones and zeros”—but do we truly grasp how our software transforms into those bits?

Both compilers and interpreters process a raw string of program code, parsing and interpreting it. While interpreters are simpler, building a basic one (handling only addition and multiplication) proves insightful. We’ll concentrate on their shared aspects: lexing and parsing input.

The Advantages and Disadvantages of Creating Your Own Interpreter

You might wonder, What’s the issue with using a regex? While powerful, regular expressions can’t handle the complexity of source code grammars. The same applies to domain-specific languages (DSLs), such as custom authorization expressions a client might require. Even without direct application, building an interpreter provides a deeper appreciation for the work behind programming languages, file formats, and DSLs.

Manually writing accurate parsers can be complex due to numerous edge cases. That’s where tools like ANTLR come in, generating parsers for common programming languages. Additionally, parser combinator libraries allow developers to write parsers directly in their chosen language, such as FastParse for Scala and Parsec for Python.

We advise using such tools and libraries professionally to avoid redundant effort. However, understanding the intricacies and possibilities of building an interpreter from scratch helps developers utilize these solutions more effectively.

Interpreter Component Overview

An interpreter comprises multiple stages:

A lexer transforms a character sequence (plain text) into a token sequence.
A parser then processes the token sequence, generating an abstract syntax tree (AST) based on formal grammar rules.
An interpreter executes the AST of the source code directly, without prior compilation.

Instead of a complete, integrated interpreter, we’ll explore each component and common issues through separate examples. Ultimately, the user code will resemble this:

1
2
3
4
5
val input = "2 * 7 + 5"
val tokens = Lexer(input).lex()
val ast = Parser(tokens).parse()
val res = Interpreter(ast).interpret()
println(s"Result is: $res")

Following the three stages, this code should calculate and display Result is: 19. We’re using Scala for its:

Conciseness, allowing ample code on screen.
Expression-oriented nature, eliminating uninitialized/null variables.
Type safety, with robust collections, enums, and case classes.

We’re specifically using Scala3’s optional-braces syntax (Python-like, indentation-based). However, none of the approaches are Scala-specific, and its similarity to other languages allows easy conversion. Alternatively, examples can be run online via Scastie.

Finally, the Lexer, Parser, and Interpreter sections use different example grammars. As the corresponding GitHub repo demonstrates, later examples have slightly adjusted dependencies for these grammars, but the core concepts remain consistent.

Interpreter Component 1: Lexer Creation

Let’s lex the string: "123 + 45 true * false1". It contains various token types:

Integer literals
A + operator
A * operator
A true literal
An identifier, false1

We’ll ignore whitespace between tokens in this example.

At this stage, expression validity isn’t important; the lexer simply converts the input string into a token list. (Parsing for meaning is the parser’s job.)

We’ll represent a token with:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
case class Token(
  tpe: Token.Type,
  text: String,
  startPos: Int
)

object Token:
  enum Type:
    case Num
    case Plus
    case Times
    case Identifier
    case True
    case False
    case EOF

Each token has a type, textual representation, and position in the input, aiding debugging for end users.

The EOF token signifies input end. It’s not present in the source text but simplifies parsing.

Our lexer should output:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
Lexing input:
123 + 45 true * false1

Tokens:
List(
  Token(tpe = Num, text = "123", tokenStartPos = 0),
  Token(tpe = Plus, text = "+", tokenStartPos = 4),
  Token(tpe = Num, text = "45", tokenStartPos = 6),
  Token(tpe = True, text = "true", tokenStartPos = 9),
  Token(tpe = Times, text = "*", tokenStartPos = 14),
  Token(tpe = Identifier, text = "false1", tokenStartPos = 16),
  Token(tpe = EOF, text = "<EOF>", tokenStartPos = 22)
)

Let’s analyze the implementation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Lexer(input: String):

  def lex(): List[Token] =
    val tokens = mutable.ArrayBuffer.empty[Token]
    var currentPos = 0
    while currentPos < input.length do
      val tokenStartPos = currentPos
      val lookahead = input(currentPos)
      if lookahead.isWhitespace then
        currentPos += 1 // ignore whitespace
      else if lookahead == '+' then
        currentPos += 1
        tokens += Token(Type.Plus, lookahead.toString, tokenStartPos)
      else if lookahead == '*' then
        currentPos += 1
        tokens += Token(Type.Times, lookahead.toString, tokenStartPos)
      else if lookahead.isDigit then
        var text = ""
        while currentPos < input.length && input(currentPos).isDigit do
          text += input(currentPos)
          currentPos += 1
        tokens += Token(Type.Num, text, tokenStartPos)
      else if lookahead.isLetter then // first must be letter
        var text = ""
        while currentPos < input.length && input(currentPos).isLetterOrDigit do
          text += input(currentPos)
          currentPos += 1
        val tpe = text match
          case "true"  => Type.True // special casing literals
          case "false" => Type.False
          case _       => Type.Identifier
        tokens += Token(tpe, text, tokenStartPos)
      else
        error(s"Unknown character '$lookahead' at position $currentPos")

    tokens += Token(Type.EOF, "<EOF>", currentPos) // special end marker
    tokens.toList

Starting with an empty token list, we iterate through the string, adding tokens as encountered.

We use the lookahead character to determine the next token’s type. Note that the lookahead character isn’t always the furthest one examined. Based on it, we determine the token’s structure and use currentPos to scan all expected characters in the current token before adding it to the list.

Whitespace is skipped. Single-letter tokens are straightforward, added while incrementing the index. For integers, we manage the index.

Now, the slight complexity: identifiers versus literals. We take the longest possible match and check if it’s a literal; otherwise, it’s an identifier.

Operators like < and <= require looking ahead one more character for = before concluding it’s a <= operator, otherwise it’s just <.

With that, our lexer produces a token list.

Interpreter Component 2: Parser Creation

We need to structure our tokens—a list alone isn’t enough. We need to know:

Expression nesting, operator application order, and applicable scoping rules.

A tree structure supports nesting and ordering. First, we define rules for constructing these trees, aiming for an unambiguous parser that consistently returns the same structure for a given input.

Note: the following parser doesn’t use the previous lexer example. It’s for adding numbers, so its grammar has only two tokens, '+' and NUM:

1
2
expr -> expr '+' expr
expr -> NUM

Equivalently, using a pipe character (|) for “or” like in regular expressions:

1
expr -> expr '+' expr | NUM

Both versions have two rules: summing two exprs or defining expr as a NUM token (nonnegative integer here).

Formal grammars define these rules. They consist of: The rules themselves A starting rule (conventionally the first one) Two symbol types for rule definition: Terminals: our language’s “letters” (and other characters)—irreducible symbols forming tokens Nonterminals: intermediate parsing constructs (replaceable symbols)

Only a nonterminal can be on a rule’s left side; the right side can have both. Above, the terminals are '+' and NUM, the only nonterminal is expr. In Java, terminals are like 'true', '+', Identifier, '[', while nonterminals are like BlockStatements, ClassBody, MethodOrFieldDecl.

We’ll use a “recursive descent” parsing technique—common due to its simplicity in understanding and implementation.

A recursive descent parser utilizes one function per grammar nonterminal. It starts from the starting rule, descending and determining the applicable rule within each function. Recursion is crucial, enabling nested nonterminals! Regexes fall short here: they can’t even handle balanced parentheses. We need a more powerful tool.

A parser for the first rule might look like this (full code):

1
2
3
4
def expr() = 
  expr()
  eat('+')
  expr()

The eat() function checks if the lookahead matches the expected token and advances the lookahead index. However, this won’t work yet due to grammar issues.

Grammar Ambiguity

Our grammar has an ambiguity, which might not be immediately obvious:

1
expr -> expr '+' expr | NUM

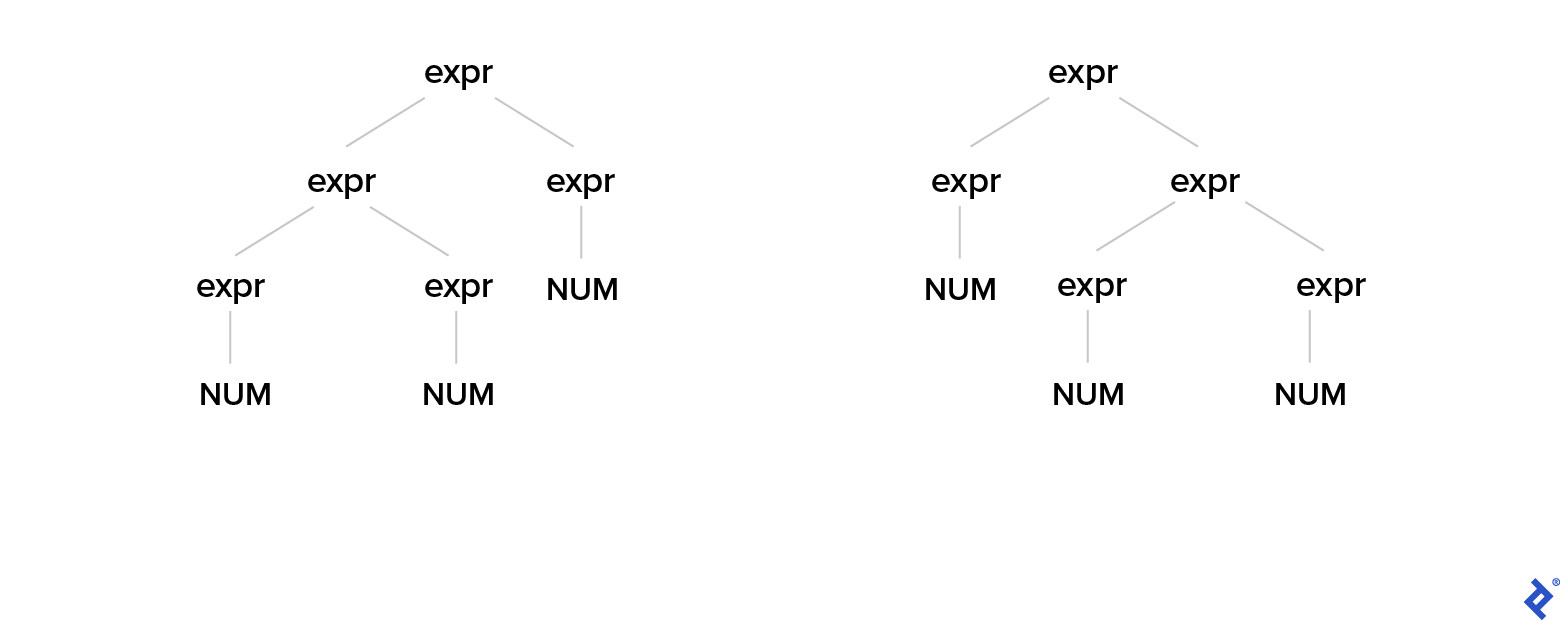
Given 1 + 2 + 3, our parser could prioritize either the left or right expr first in the AST:

Two abstract syntax trees. Both start with expr and branch left and right each to another expr, one of which branches straight down to a NUM, and the other of which branches left and right each to another expr that branches down to a NUM. The AST on the left has the larger subtree on its left expr, whereas the AST on the right has the larger subtree on its right expr. — Left-handed and right-handed ASTs.

We need to introduce asymmetry:

1
expr -> expr '+' NUM | NUM

The expressible expressions remain unchanged, but now it’s unambiguous: the parser consistently prioritizes the left side, making our + operation left associative (this becomes clearer in the Interpreter section).

Left-recursive Rules

However, this doesn’t solve our other issue, left recursion:

1
2
3
4
def expr() =
  expr()
  eat('+')
  eat(NUM)

We have infinite recursion, leading to a stack overflow. Parsing theory to the rescue!

Consider this grammar, with alpha as any terminal/nonterminal sequence:

1
A -> A alpha | B

We can rewrite it as:

1
2
A   -> B A'
A'  -> alpha A' | epsilon

Here, epsilon is an empty string—nothing, no token.

Our current grammar:

1
expr -> expr '+' NUM | NUM

Rewriting with the method above, where alpha is '+' NUM, we get:

1
2
expr    -> NUM exprOpt
exprOpt -> '+' NUM exprOpt | epsilon

Now parsable with recursive descent. Let’s see the parser for this iteration:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Parser(allTokens: List[Token]):
  import Token.Type
  
  private var tokens = allTokens
  private var lookahead = tokens.head
  
  def parse(): Unit = 
    expr()
    if lookahead.tpe != Type.EOF then
      error(s"Unknown token '${lookahead.text}' at position ${lookahead.tokenStartPos}")

  private def expr(): Unit =
    eat(Type.Num)
    exprOpt()
  
  private def exprOpt(): Unit =
    if lookahead.tpe == Type.Plus then
      eat(Type.Plus)
      eat(Type.Num)
      exprOpt()
    // else: end recursion, epsilon
  
  private def eat(tpe: Type): Unit =
    if lookahead.tpe != tpe then
      error(s"Expected: $tpe, got: ${lookahead.tpe} at position ${lookahead.startPos}")
    tokens = tokens.tail
    lookahead = tokens.head

We use the EOF token for simplicity, ensuring at least one token in our list, avoiding empty list handling.

With a streaming lexer, we wouldn’t have an in-memory list but an iterator, requiring a marker for input end. At the end, the EOF token should be last.

Analyzing the code, an expression can be a single number. If nothing remains, the next token wouldn’t be Plus, stopping parsing. The last token would be EOF.

With more tokens, they must be like + 123, triggering recursion on exprOpt()!

AST Generation

Our parsed expression is difficult to work with as is. We could use callbacks in the parser, but that becomes cumbersome. Instead, we return an AST, a tree representing the expression:

1
2
3
4
5
case class Expr(num: Int, exprOpt: ExprOpt)

enum ExprOpt:
  case Opt(num: Int, exprOpt: ExprOpt)
  case Epsilon

This mirrors our rules using data classes.

Our parser now returns a usable data structure:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Parser(allTokens: List[Token]):
  import Token.Type
  
  private var tokens = allTokens
  private var lookahead = tokens.head
  
  def parse(): Expr = 
    val res = expr()
    if lookahead.tpe != Type.EOF then
      error(s"Unknown token '${lookahead.text}' at position ${lookahead.tokenStartPos}")
    else
      res

  private def expr(): Expr =
    val num = eat(Type.Num)
    Expr(num.text.toInt, exprOpt())
  
  private def exprOpt(): ExprOpt =
    if lookahead.tpe == Type.Plus then
      eat(Type.Plus)
      val num = eat(Type.Num)
      ExprOpt.Opt(num.text.toInt, exprOpt())
    else
      ExprOpt.Epsilon

For eat(), error(), and other details, see the accompanying GitHub repo.

Simplifying Rules

Our ExprOpt nonterminal can be improved:

1
'+' NUM exprOpt | epsilon

Its grammar pattern isn’t immediately clear. We can replace this recursion:

1
('+' NUM)*

This means '+' NUM occurs zero or more times.

Our complete grammar now:

1
2
expr  -> NUM exprOpt*
exprOpt -> '+' NUM

And a cleaner AST:

1
2
case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(num: Int)

The resulting parser is the same length but more understandable. We’ve eliminated Epsilon, implied by starting with an empty structure.

We didn’t need the ExprOpt class here. We could have used case class Expr(num: Int, exprOpts: Seq[Int]), or NUM ('+' NUM)* in grammar format. Why didn’t we?

Consider multiple operators like - and *:

1
2
expr  -> NUM exprOpt*
exprOpt -> [+-*] NUM

Here, the AST needs ExprOpt to accommodate the operator type:

1
2
case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(op: String, num: Int)

Note: [+-*] in the grammar is like regular expressions: “one of these characters,” as we’ll soon see.

Interpreter Component 3: Interpreter Creation

Our interpreter utilizes the lexer and parser to obtain the AST of our input expression and evaluate it accordingly. Here, we’re dealing with numbers and want to calculate their sum.

In the implementation of our interpreter example, we’ll use this grammar:

1
2
expr  -> NUM exprOpt*
exprOpt -> [+-] NUM

And this AST:

1
2
case class Expr(num: Int, exprOpts: Seq[ExprOpt])
case class ExprOpt(op: Token.Type, num: Int)

(Lexer and parser implementations for similar grammars were covered; if needed, refer to the repo for this specific grammar.)

Let’s write an interpreter for the above grammar:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Interpreter(ast: Expr):

  def interpret(): Int = eval(ast)

  private def eval(expr: Expr): Int =
    var tmp = expr.num
    expr.exprOpts.foreach { exprOpt =>
      if exprOpt.op == Token.Type.Plus
      then tmp += exprOpt.num
      else tmp -= exprOpt.num
    }
    tmp

Successfully parsing into an AST guarantees at least one NUM. We then add (or subtract) the optional numbers to our result.

The earlier note about +’s left associativity is now clear: We start from the leftmost number and add others sequentially. While seemingly trivial for addition, consider subtraction: 5 - 2 - 1 evaluates as (5 - 2) - 1 = 3 - 1 = 2, not 5 - (2 - 1) = 5 - 1 = 4!

Going beyond plus and minus, we need another rule.

Precedence

Parsing 1 + 2 + 3 is simple, but 2 + 3 * 4 + 5 poses a challenge.

Conventionally, multiplication has higher precedence than addition, but our parser doesn’t inherently know this. We can’t evaluate it as ((2 + 3) * 4) + 5, but rather as (2 + (3 * 4)) + 5.

Therefore, multiplication needs evaluation first, positioned further from the AST root to ensure evaluation before addition, requiring another layer of indirection.

Fixing a Naive Grammar

Our original left-recursive grammar lacked precedence rules:

1
expr -> expr '+' expr | expr '*' expr | NUM

First, we add precedence rules and remove ambiguity:

1
2
expr    -> expr '+' term | term
term    -> term '*' NUM | NUM

Then, we apply non-left-recursive rules:

1
2
3
4
expr      -> term exprOpt*
exprOpt   -> '+' term
term      -> NUM termOpt*
termOpt   -> '*' NUM

This yields a well-structured AST:

1
2
3
4
5
case class Expr(term: Term, exprOpts: Seq[ExprOpt])
case class ExprOpt(term: Term)

case class Term(num: Int, termOpts: Seq[TermOpt])
case class TermOpt(num: Int)

Resulting in a concise interpreter:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Interpreter(ast: Expr):

  def interpret(): Int = eval(ast)

  private def eval(expr: Expr): Int =
    var tmp = eval(expr.term)
    expr.exprOpts.foreach { exprOpt =>
      tmp += eval(exprOpt.term)
    }
    tmp

  private def eval(term: Term): Int =
    var tmp = term.num
    term.termOpts.foreach { termOpt =>
      tmp *= termOpt.num
    }
    tmp

Again, the lexer and grammar ideas were previously covered; refer to find them in the repo if needed.

Further Steps in Interpreter Development

We haven’t addressed error handling and reporting, crucial aspects of any parser. Confusing compiler errors are frustrating for developers. Providing accurate error messages, avoiding message overload, and enabling graceful error recovery are important. Developers creating interpreters or compilers should prioritize a good user experience.

Our example lexers, parsers, and interpreters only scratch the surface of compiler and interpreter theory. Other topics include:

Scopes and symbol tables
Static types
Compile-time optimization
Static analyzers and linters
Code formatting and pretty-printing
Domain-specific languages

For further exploration, I recommend:

Language Implementation Patterns by Terence Parr
The free online book, Crafting Interpreters, by Bob Nystrom
Intro to Grammars and Parsing by Paul Klint
Writing Good Compiler Error Messages by Caleb Meredith
The notes from East Carolina University’s “Program Translation and Compiling” course